| Closures |
 |
 |
 |
We've seen how we can get data from our parsers using the ever so useful assign action:
int i;
integer = int_p[assign(i)];Nifty! Our rule integer, if successful, passes the parsed integer to the variable i. Everytime we need to parse an integer, we can call our rule integer and simply extract the parsed number from the variable i. There's something you should be aware of though. In the viewpoint of the grammar, the variable i is global. When the grammar gets more complex, it's hard to keep track of the current state of i. And, with recursive rules, global variables simply won't be adequate.
Closures are needed if you need your rules (or grammars) to be reentrant. For example, a rule (or grammar) might be called recursively indirectly or directly by itself. The calculator is a good example. The expression rule recursively calls itself indirectly when it invokes the factor rule.
We need a machanism to attach local variables to our rules (and grammars). Closures provide an environment, a stack frame, for local variables to reside. Most importantly, the closure variables are accessible from the EBNF grammar specification and can be used to pass parser information upstream or downstream from the topmost rule down to the terminals in a top-down recursive descent. For one, closures provide a parser with the ability to have inherited and synthetic attributes, more or less analogous to return values and function arguments.
When a rule is given a closure, the closure's local variables are created prior to entering the parse function and destructed after exiting the parse function. These local variables are true local variables that exist on the hardware stack.
Spirit v1.6.2 closure support requires Phoenix. In the future, Spirit will fully support BLL. Currently, work is underway to merge the features of both libraries. |
Declaring closures
The general closure declaration syntax is:
struct name : spirit::closure<name, type1, type2, type3..., typeN>
{
member1 m_name1;
member2 m_name2;
member3 m_name3;
...
memberN m_nameN;
}; member1... memberN are indirect links to the actual closure
variables. Their indirect types correspond to type1...
typeN. Here's an example that has two closure members:
struct my_closure : closure<my_closure, double, int>
{
member1 x;
member2 y;
};member1 and member2 are indirect links to the actual closure variables. Their indirect types correspond to double and int, respectively.
Closure return value (synthetic attribute)
The closure member1 is the closure's return value (synthetic attribute in parsing terminology). This return value, like the one returned by anychar_p, for example, can be used to propagate data up the parser hierarchy or passed to semantic actions.
Attaching closures
Closures can be applied to rules, subrules and grammars. The closure has a special parser context that can be used with these non terminals. The closure's context is its means to hook into the rule, subrule or grammar. Given the example my_closure above, we can create a rule with a closure by declaring it as:
rule<ScannerT, my_closure::context_t> r;
where ScannerT is the actual type of the scanner that we wish to use. Similarly for subrules:
subrule<ID, my_closure::context_t> sr;
And if you wish to attach a grammar:
struct my_grammar : grammar<my_grammar, my_closure::context_t>
{
/*...*/
};
my_grammar g;
Accessing closure members
Closure members can be accessed from within semantic actions just like you would struct members: by qualifying the member name with its owner rule, subrule or grammar. Examples:
r.x // refer to rule r's closure member x
sr.y // refer to subrule sr's closure member y
g.x // refer to grammar g's closure member xInitializing closure members (inherited attributes)
Closure enabled rules, subrules and grammars by default, default constructs its members when the host rule, subrule or grammar enters its parse member function. If this is not desirable, we can pass constructor arguments (inherited attributes in parsing terminology) to the rule, subrule or grammar. The syntax mimics a function call. For example, if you wish to construct my_closure's members to 3.6 and 8, respectively, when we invoke the rule r, we write:
r(3.6, 8) // invoke rule r and set its closure members to 3.6 and 8The constructor arguments are actually Phoenix lambda expressions, so you can use arbitrarily complex expressions such as:
// invoke rule r and set its closure members to (g.x / 8) * g.y and 0
// where g.x and g.y are the closure members of grammar g in our example
// above
r((g.x / 8) * g.y, 0)We can pass less arguments than the actual number of members in the closure. The members at the right with no corresponding constructor arguments are default constructed. Example:
r(11.9) // invoke rule r and set its closure members to 11.9 and 0Passing more arguments than there are closure members is an error.
Consider a rule that parses even palindromes: A parser that can recognize textual mirror images such as "abcddcba".
Without closures, this can be achieved by setting up a stack, pushing the first parsed character into the stack, then recursively calling itself. Upon exit, from the recursion, the pushed character from the stack is popped and used to recognize the next parsed character to match. |
Let's declare our closure. We need only one closure member, a char :
struct my_closure : spirit::closure<my_closure, char>
{
member1 ch;
};
Remember rule and grammar contexts? This is the closure's means to hook into the grammar and rule. The closure has a special parser context that may be used to enable rule, subrule and grammar closures.
rule<scanner<>, my_closure::context_t> rev;
Declares a rule rev with our closure.
rev = anychar_p[rev.ch = arg1] >> !rev >> fch_p(rev.ch);
Defines our even palindrome parser.
1) anychar_p parses any character and assigns it to rev's
sole closure member rev.ch. Using Phoenix,
the result of anychar_p is assigned to rev.ch. What is arg1?
If at this point, you are not familiar with lambda expressions yet, I suggest
you take a quick peek at: Phoenix
Place-holders. Anyway, it is a placeholder for the first argument that the
semantic action will receive:
anychar_p[rev.ch = arg1]
2) Then, rev recursively calls itself:
>> !rev
Finally,
fch_p(rev.ch)
3) attempts to recognize the character we just stored in rev.ch. Take note that fch_p is very similar to ch_p but accepts functors such as closure member accesses (see Parametric Parsers).
In Boost.Lambda (BLL), arg1 corresponds to _1. |
What are Closures?
The closure as an object that "closes" over the local variables of a function making them visible and accessible outside the function. What is more interesting is that the closure actually packages a local context (stack frame where some variables reside) and makes it available outside the scope in which they actually exist. The information is essentially "captured" by the closure allowing it to be referred to anywhere and anytime, even prior to the actual creation of the variables.
The following diagram depicts the situation where a function A (or rule) exposes its closure and another function B references A's variables through its closure.
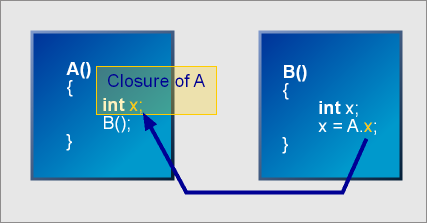 |
| The
closure as an object that "closes" over the local variables
of a function making them visible and accessible outside the function |
Of course, function A should be active when A.x is referenced. What this means is that function B is reliant on function A (If B is a nested function of A, this will always be the case). The free form nature of Spirit rules allows access to a closure variable anytime, anywhere. Accessing A.x is equivalent to referring to the topmost stack variable x of function A. If function A is not active when A.x is referenced, a runtime exception will be thrown.
Nested Functions
To fully understand the importance of closures, it is best to look at a language such as Pascal which allows nested functions. Since we are dealing with C++, lets us assume for the moment that C++ allows nested functions. Consider the following pseudo C++ code:
void a() { int va; void b() { int vb; void c() { int vc; } c(); } b(); }
We have three functions a, b and c where c is nested in b and b is nested in a. We also have three variables va, vb and vc. The lifetime of each of these local variables starts when the function where it is declared is entered and ends when the function exits. The scope of a local variable spans all nested functions inside the enclosing function where the variable is declared.
Going downstream from function a to function c, when function a is entered, the variable va will be created in the stack. When function b is entered (called by a), va is very well in scope and is visble in b. At which point a fresh variable, vb, is created on the stack. When function c is entered, both va and vb are visibly in scope, and a fresh local variable vc is created.
Going upstream, vc is not and cannot be visible outside the function c. vc's life has already expired once c exits. The same is true with vb; vb is accessible in function c but not in function a.
Nested Mutually Recursive RulesNow consider that a, b and c are rules:
a = b >> *(('+' >> b) | ('-' >> b)); b = c >> *(('*' >> c) | ('/' >> c)); c = int_p | '(' >> a >> ')' | ('-' >> c) | ('+' >> c);
We can visualize a, b and c as mutually recursive functions where a calls b, b calls c and c recursively calls a. Now, imagine if a, b and c each has a local variable named value that can be referred to in our grammar by explicit qualification:
a.value // refer to a's value local variable b.value // refer to b's value local variable c.value // refer to c's value local variable
Like above, when a is entered, a local variable value is created on the stack. This variable can be referred to by both b and c. Again, when b is called by a, b creates a local variable value. This variable is accessible by c but not by a.
Here now is where the analogy with nested functions end: when c is
called, a fresh variable value is created which, as usual, lasts the
whole lifetime of c. Pay close attention however that c may
call a recursively. When this happens, a may now refer to
the local variable of c.
 |
 |
 |
Copyright © 1998-2003 Joel de Guzman
Distributed under the Boost Software License, Version 1.0.
(See accompanying file LICENSE_1_0.txt or copy at
http://www.boost.org/LICENSE_1_0.txt)